 The global market for hardware encryption solutions is expected to reach $413.85 billion by the year 2022 according to market research published by Markets and Markets. This total represents a compound annual growth rate (CAGR) of 29.3 percent between 2016 and 2022. The global market for public key infrastructure, a portion of the encryption market which utilizes public keys to encrypt and authenticate information that is transferred electronically, is expected to grow at a 22.7 CAGR between 2015 and 2023 when it will reach global revenues of $1.99 billion, according to research published by Market Research Future.
The global market for hardware encryption solutions is expected to reach $413.85 billion by the year 2022 according to market research published by Markets and Markets. This total represents a compound annual growth rate (CAGR) of 29.3 percent between 2016 and 2022. The global market for public key infrastructure, a portion of the encryption market which utilizes public keys to encrypt and authenticate information that is transferred electronically, is expected to grow at a 22.7 CAGR between 2015 and 2023 when it will reach global revenues of $1.99 billion, according to research published by Market Research Future.
One of the first and most widely-used public key systems for cryptography is known as RSA cryptography, named for the trio of inventors who developed the system at the Massachusetts Institute of Technology in the late 1970s: Ronald Rivest, Adi Shamir and Leonard Adleman. These three inventors have each been inducted as part of the 2018 class of the National Inventors Hall of Fame and this Thursday, September 20th, marks the 35th anniversary of the issue of the seminal patent in the field of RSA cryptography. With this important date upon us, we return to our Evolution of Technology series to explore the development of this encryption system which has been incorporated as a fundamental aspect of many transaction systems and secure communications protocols.
History of Public Key Cryptography from the Polybius Grid to the Diffie-Hellman Key Exchange
Although cryptography is a field which has greatly expanded thanks to the proliferation of digital communications, the use of ciphers to maintain the secrecy of messages actually dates back to the ancient Greek scholar Polybius. Living in the 2nd century BC, Polybius developed a grid system in which letters could be represented by numbers with the idea that messages could be conveyed over distances using torches to indicate the numbers associated with letters. Less than a century later, the famed Roman emperor Julius Caesar used a method of private key encryption for messages sent including critical military commands. Caesar employed a simple system of shifting letters of the alphabet by a few positions, such as substituting D for A, E for B, and so on, to make his messages unintelligible to enemy forces.
By the 19th century, early methods of public key cryptography systems were theorized by the British mathematician and logician William Stanley Jevons. In his book The Principles of Science, first published in 1874, he discussed how the factorization of extremely high numbers which were 10 digits long could be useful in keeping secret the identity of the two numbers which were multiplied to achieve the long string of digits. This is an early model of a trapdoor function, or a function easy to compute in one direction but nearly impossible to compute in the opposite direction without knowledge of the numbers used in the original computation, which is an essential function of many modern-day encryption systems.
The development of public key encryption systems would make major advances beginning in the early 1970s with the work of British cryptologist James Ellis conceived of the possibility of non-secret encryption methods using publicly available numbers as keys. A few years later, British mathematician Clifford Cocks developed an early version of what became the RSA encryption system, although the work was classified and kept secret by both the British and U.S. governments. In 1976, American cryptologists Whitfield Diffie and Martin Hellman developed a method known as the Diffie-Hellman key exchange which used asymmetric keys to authenticate communications over a channel.
Rivest, Shamir and Adleman Develop RSA Cryptography
Prior to joining MIT, Rivest earned his bachelor’s degree in mathematics from Yale University in 1969 and obtained his Ph.D. in computer science from Stanford University in 1974. Adleman received his education from the University of California, Berkeley, where he obtained both his bachelor’s in mathematics in 1968 and his Ph.D. in electrical engineering and computer science in 1976. Shamir, who was born in Tel Aviv, Israel, received his bachelor’s degree in mathematics from Tel Aviv University in 1973 and his Ph.D. in computer science in 1977 from the Weizmann Institute.
Working together at MIT, this trio of inventors expanded upon the work of Diffie and Hellman to create what would become the world’s most widely used method of public-key encryption for securing communications over the Internet. The RSA encryption system enables a user to create and publish a public key which is the product of two prime numbers which are kept secret from others. The public key can be used by anyone to encode messages but knowledge of the two prime numbers are required for the decryption of those encoded messages. The RSA method improved upon previous systems by providing means for encryption and decryption which don’t rely on both parties having a shared secret key. Rivest and Shamir worked to develop the public key system and Adleman helped by trying to break each system developed by the other two inventors. It took 42 attempts for the trio to find a public key system which was unbreakable.
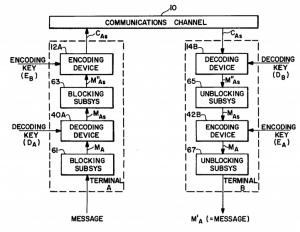 The groundbreaking work contributed by this trio of inventors is reflected in the issue of U.S. Patent No. 4405829, titled Cryptographic Communications System and Method and issued on September 20th, 1983. It claimed a cryptographic communications system having a communications channel, an encoding means coupled to the channel and adapted for transforming a transmit message word signal M to a ciphertext word signal C transmitted on the channel where M is formed from a composite number of two prime numbers p and q and C corresponds to the M value modified by a number relatively prime to 1 cm(p-1, q-1), and then a decoding means coupled to the channel that transforms C to a receive message word signal M’ that corresponds to a number representative of a deciphered form of C. The resulting invention provided a system and method for establishing a private communications system for the transmission of signed messages through the implementation of a public key cryptographic communications system.
The groundbreaking work contributed by this trio of inventors is reflected in the issue of U.S. Patent No. 4405829, titled Cryptographic Communications System and Method and issued on September 20th, 1983. It claimed a cryptographic communications system having a communications channel, an encoding means coupled to the channel and adapted for transforming a transmit message word signal M to a ciphertext word signal C transmitted on the channel where M is formed from a composite number of two prime numbers p and q and C corresponds to the M value modified by a number relatively prime to 1 cm(p-1, q-1), and then a decoding means coupled to the channel that transforms C to a receive message word signal M’ that corresponds to a number representative of a deciphered form of C. The resulting invention provided a system and method for establishing a private communications system for the transmission of signed messages through the implementation of a public key cryptographic communications system.
In 1982, one year prior to the granting of the ‘829 patent, the three inventors co-founded the network security company RSA Security. In 1995, RSA Security opened a new division called Digital Certificates International, which eventually became known as the network security firm Verisign. RSA Security was acquired by EMC Corporation in 2006 for about $2.1 billion and is currently part of the Dell Technologies family of brands after EMC was acquired by Dell in 2016.
For their work in cryptography, Rivest, Shamir and Adleman share the 2002 Turing Award. Both Rivest and Adleman would go on to become members of the National Academy of Engineering and the National Academy of Sciences. Shamir also received a number of additional honors and recognitions throughout his career, including the Israel Mathematical Society’s Erd?s Prize as well as the 2008 Israel Prize for computer sciences. Rivest continues to serve as an Institute Professor at MIT while Shamir would go on to contribute to computational complexity theory and Adleman went on to create the field of DNA computing.
Image Source: Deposit Photos.

![[IPWatchdog Logo]](https://ipwatchdog.com/wp-content/themes/IPWatchdog%20-%202023/assets/images/temp/logo-small@2x.png)

![[[Advertisement]]](https://ipwatchdog.com/wp-content/uploads/2024/04/Patent-Litigation-2024-banner-938x313-1.jpeg)



![[Advertisement]](https://ipwatchdog.com/wp-content/uploads/2024/04/Artificial-Intelligence-2024-REPLAY-sidebar-700x500-corrected.jpg)
![[Advertisement]](https://ipwatchdog.com/wp-content/uploads/2024/04/Patent-Litigation-Masters-2024-sidebar-700x500-1.jpg)

![[Advertisement]](https://ipwatchdog.com/wp-content/uploads/2021/12/WEBINAR-336-x-280-px.png)
![[Advertisement]](https://ipwatchdog.com/wp-content/uploads/2021/12/2021-Patent-Practice-on-Demand-recorded-Feb-2021-336-x-280.jpg)
![[Advertisement]](https://ipwatchdog.com/wp-content/uploads/2021/12/Ad-4-The-Invent-Patent-System™.png)






Join the Discussion
5 comments so far.
LazyCubicleMonkey
September 30, 2018 07:54 pm@Anon
Can you describe the difference between the 3 in detail?
What about a set of multivariable equations (solved via matrix math) that when solved would produce some set of constants that could be used in a patentable invention – what category would that be in? Would the implementation of this solution in software be patentable? Should it be?
angry dude
September 20, 2018 04:06 pm“Math”, although much more complex than RSA algo, is the key to any digital signal/image processing patent of any value
Pass raw digitized audio/video signal through compression algo, transmit it over distance or store it, then uncompress it
It’s all MATH and when claimed properly to achieve full scope of coverage (which is not known in advance) you can even call it “abstract math”
Those scotus critters are science illiterate and should be impeached
alas… not gonna happen
Night Writer
September 20, 2018 04:03 pm@1 Ternary
Really good point.
Anon
September 20, 2018 02:15 pmThree distinct items:
math
applied math
Math(S)
Ternary
September 20, 2018 09:33 amNice article Steve. Unfortunately, you don’t explain the basic mathematical operation that enables PKI methods like Diffie-Hellman and RSA. That mathematical operation is modulo-n arithmetic and mainly modulo-n multiplication. For instance 3 times 5 is 15, but 3 times 5 modulo-7 is 1. This simple fact causes a discrete multiplicative inverse to exist. (the ‘normal’ multiplicative inverse of 3 is of course 1/3 or .3333 and basically unusable in cryptography). In case of modular multiplication modulo-7, the multiplicative inverse of 3 is 5. Furthermore, factorizing large modulo-n numbers becomes very time consuming. There are some other properties of modulo-n arithmetic that are significant, but that is not really the point here.
The fact is that PKIs like Diffie-Hellman and RSA rely on very basic arithmetical operations such as modulo-n multiplication, but on very large numbers and performed many times.
You correctly highlight the enormous significance and economic value of cryptographic hardware and PKI infrastructure. It is to me inconceivable that almost every patent application in the field of encryption, PKI and authentication is at least initially rejected over Alice based on the fact of the use of a mathematical operation.
I only know of one case where the Examiner opined that an Alice/Mayo analysis was warranted and that even though mathematics was applied it was well known that cryptography offered significant more than a mere mathematical operation and thus declared the claimed invention patent eligible. Bravo! Not many of those with fortitude in the USPTO.
The USPTO should issue a memo on this subject, like in Berkheimer, to make sure that inventors in the critical field of cryptography are not discouraged in this eminently important field to pursue patent protection by unwarranted Alice rejections.